Geometry in real life
 The word “Geometry” is derived from the Greek word “Geo” and “Metron” which mean Earth and Measurement respectively.
Translating roughly to “Earth’s Measurement,” geometry is primarily concerned with the characteristics of figures as well as shapes.
Practically, geometry plays a great role in determining the areas, volumes, and lengths.
Euclid is considered to be the “Father of Geometry.”
The word “Geometry” is derived from the Greek word “Geo” and “Metron” which mean Earth and Measurement respectively.
Translating roughly to “Earth’s Measurement,” geometry is primarily concerned with the characteristics of figures as well as shapes.
Practically, geometry plays a great role in determining the areas, volumes, and lengths.
Euclid is considered to be the “Father of Geometry.”

Since birth, humans are attracted to diverse shapes, designs, and colours. The aforesaid can be reinforced by the fact that while buying things in the market, humans are allured by fabrics with fascinating patterns, books with eye-catching covers, sunglasses of one-of-its-kind shapes, jewellery with captivating patterns, tea mugs with beautiful forms, and what-not! Geometry can be referred to as being “omnipresent.” Moreover, geometrical shapes of different toys play an utterly crucial role in the development of the cognitive skills in children during the early stages of their growth. Let’s discuss some important examples of geometry which do not fail even a single chance to play a pivotal role in the daily life of humans.
1. Nature

The most important example of geometry in everyday life is formed by the nature surrounding humans. If one looks closely, one might find different geometrical shapes and patterns in leaves, flowers, stems, roots, bark, and the list goes on. The organisation of the human digestive system as a tube within a tube also ascertains the role of geometry. The leaves on the trees are of varying shapes, sizes, and symmetries. Different fruits and vegetables have different geometrical shapes; take the example of orange, it is a sphere and after peeling it, one might notice how the individual slices form the perfect sphere.

Looking closely at a honeycomb, one will see hexagonal patterns arranged tandemly. Similarly, examining a snowflake under a microscope will enable the examiner to be the guest of beautiful geometrical patterns.

The next interesting example of the role of geometry in nature is formed by the pattern popularly known as “Six-Around-One.” The flowers exhibit the “six-around-one” patterns, also called “Closest Packing of Circles,” “Hexagonal Packaging,” and “Tessellating Hexagons.”
2. Technology

The most common example of geometry in everyday life is technology. Be it robotics or computers or video games, geometry is applied to almost all the underlying concepts. The computer programmers are able to work because the concepts of geometry are always at their disposal. The virtual world of video games is created only because the geometric computations help in designing of the complex graphics of the video games. Raycasting, the process of shooting, employs a 2-D map for stimulating the 3-D world of the video games. Raycasting helps in increasing processing as the calculations are carried out for the vertical lines on the screen.
3. Homes

Geometry does not leave even a single chance to play a significant in homes as well. The windows, doors, beds, chairs, tables, TV, mats, rugs, cushions, etc have different shapes. Moreover, bedsheets, quilts, covers, mats, and carpets have different geometric patterns on them. Geometry is also important cooking. The chef needs to add all the ingredients in accurate proportions and ratio to put forth a delicious dish. Also, while organising a room, each and every space is utilised to make the room look more appealing. A house is made to look more presentable by using vases, paintings, and various decorative pieces, which are of different geometric shapes and have different patterns made on them.
4. Architecture
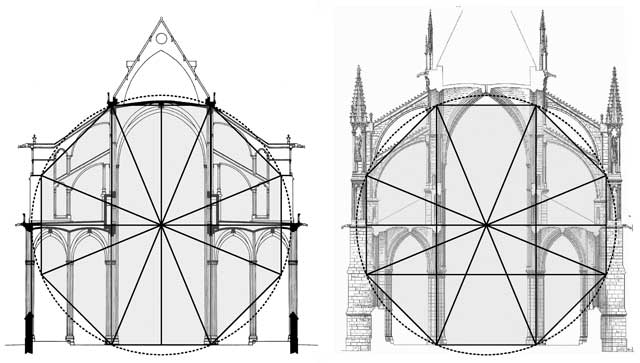
The construction of various buildings or monuments has a close relationship with geometry. Before constructing architectural forms, mathematics and geometry help put forth the structural blueprint of the building. The theories of proportions and symmetries shape the fixed aspects for all kinds of architectural designs. Pythagoras’ “Principles of Harmony” along with geometry were employed in the architectural designs of sixth century BC. Not only were the basics of mathematics coupled with geometry helped in increasing the aesthetics, harmony, and the religious value of large structures but also aided in mitigating various hazards resulting from high-speed winds.

Moreover, the staircase in all the buildings take into consideration the angles of geometry and are constructed at 90 degrees.
5. Art

What does art include? Art encompasses the formation of figures & shapes, a basic understanding of 2-D & 3-D, knowledge about spatial concepts, and contribution of estimation, patterns & measurement. From the aforesaid, it is evident that there is a close relationship between art and geometry. The formation of shapes is a result of the use of geometrical forms like circle, triangle, square, mandala, or octagon. Moreover, the contents of paintings or sculptures are largely affected by the choice and shape of frames. Not to forget that the principles of projective geometry form the basis of perspective, which is used in most of the painting.
6. Sports

Sports often does not fail a sole chance to make use of geometrical concepts. The buildings of the sports stadiums and athletic fields take into consideration geometric shapes. The athletic fields also employ geometry; hockey, soccer, basketball, and football fields are rectangular in shape. The corner kick spots, goal posts, arcs, D-section, and centre circle are marked on the field. Similarly, the pitches of various other sports like volleyball and basketball take into consideration the geometrical aspects because these pitches have oval as well as circular arcs marked clearly. Talking of track field, semicircular shapes are often noticeable. Angles also play a critical role in predicting the movement of the players, enhancing their performance, and scoring a point.
7. Designing

Geometry is widely applied in the field of designing; the creation of animated figures in the video games require geometry. In the case of art, almost every element of designing is entwined with geometric proportions, which is used to depict a story. Taking the examples of miniature paintings and manuscript illumination, geometric principles are employed to compose the layout. Strict geometric proportions are paid attention to while forming individual letters in calligraphy. In designing, geometry has a symbolic role to play; as is evident from the carvings on the walls, roofs, and doors of various architectural marvels.
8. Computer Aided Design- CAD
Geometry, one of the principle concepts of mathematics, entails lines, curves, shapes, and angles. Before any architectural design is made, a computer software helps in rendering visual images on the screen. CAD, a software, puts forth the blueprint of the design. Moreover, it also aids in the simulation of the architectural forms which allows for the better understanding of the finished product. The principles of geometry are being used extensively in various industrial processes which allows the designing of graphics.
9. Mapping

Geometry helps in the accurate calculation of the physical distances. It is employed in the field of astronomy to map the distances between stars & planets and between different planets. It also aids in the determination of a relationship between the movements of different bodies in the celestial environment. Apart from mapping distances between celestial bodies, geometry also plays a vital role in surveying and navigation. In the case of surveying, measurement of the area of land is a result of the accurate determination of the shape of the land. Moreover, in navigation, the ships, watercraft, and aircraft utilise angles and also depend on other mathematical concepts for carrying out basic operations.
10. Medicine

Techniques like x-rays, ultrasounds, MRIs, and nuclear imaging require the reconstruction of shapes of organs, bones, and tumours, which is based on geometry only. Physiotherapy also employs geometry. Geometric properties and features help in defining the image in digital grids. The geometrical concepts not only aid in visualization, manipulation, image segmentation, correction, and object representation but also play an important role in increasing stability, fidelity, and efficiency. Bisecting angle techniques and parallel techniques are crucial in radiology.
11. Geographic Information Systems

The GPS of the satellites use geometrical principles to calculate the position of the satellites. The use of coordinate geometry in the Global Positioning System (GPS) provides precise information about the location and time. GPS employes coordinates to calculate the distance between any two places. The coordinate geometry helps GPS to track transportation accidents and carry out rescue operations. The coordinate geometry also aids in enhancing flight security weather forecasting, earthquake monitoring, and environmental protection. Moreover, various facets of military operations are equipped with GPS.
source: https://studiousguy.com/examples-of-geometry-in-everyday-life/





0 General Document comments
0 Sentence and Paragraph comments
0 Image and Video comments
New Conversation
Hide Thread Detail
General Document Comments 0

